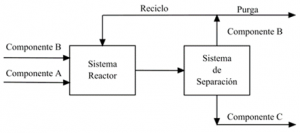Importancia y contexto – Con la disponibilidad de significativamente mayores capacidades de procesamiento en las nuevas generaciones de computadoras, los modelos simulados de plantas de proceso que pueden desarrollarse son hoy muchos más detallados y sistémicos. La solución de problemas de síntesis y diseño requieren incluir en los problemas de optimización asociados representaciones de la incertidumbre estructural y paramétrica del modelo simulado. Por la complejidad matemática y la demanda computacional asociada, para ser integrados dentro de un problema de optimización estos modelos demandan un enfoque alternativo a la programación matemática convencional. Particularmente, en procesos donde existe una elevada integración energética con presencia de recirculación de materia (Figura), la optimización basada en el uso de un modelo simulado es particularmente difícil, lo que representa un obstáculo a la hora de resolver formulaciones más realistas de los problemas de síntesis y diseño.

Problemática – La problemática de la programación matemática aplicada a la solución de programas matemáticos del tipo MINLP no convexos radica en la dificultad que tienen los métodos de optimización convencionales (Solvers) en hallar un punto óptimo global en la región factible del problema y la difícil convergencia cuando se trata de modelos simulados detallados que incorporan incertidumbre. En la optimización Bayesiana, el modelo simulado se trata como una “caja negra” con entradas correspondientes a los variables de decisión (síntesis & diseño) y las variables no controladas representativas de la incertidumbre. La optimización Bayesiana genera una secuencia breve de “experimentos simulados” con distintas combinaciones de las variables de decisión. Se parte de una serie de puntos evaluados sobre la base de los cuales se ajusta un meta-modelo de la función objetivo. La búsqueda del nuevo punto óptimo se basa en la probabilidad de que el mismo sea efectivamente el máximo de una función de mejora (adquisition funcition) considerando la incertidumbre con la predicción del meta-modelo del simulador.

Objetivos – El objetivo de esta temática de tesis doctoral es desarrollar nuevos algoritmos de optimización Bayesiana y ensayarlos computacionalmente en el campo de la síntesis, diseño y optimización sistémica de plantas químicas, que en la actualidad es un área de excelencia en la ingeniería de procesos. Se aspira a que el uso de la optimización Bayesiana represente una opción factible a la hora de optimizar un proceso usando un simulador detallado del mismo.

Contacto: Dr. Carlos D. Fischer; Dr. Ernesto Martínez (ra.vo1732214243g.tec1732214243inoc-1732214243efatn1732214243as@ra1732214243gnIsa1732214243ceb1732214243)